SPC 並非僅僅是圖表和公式的堆砌,其背後蘊含著深奧的統計學原理。讓我們深入淺出地介紹 SPC 所依賴的基本統計學概念,幫助大家理解 SPC 如何成為現代品質管理的重要工具。
SPC 是一種利用統計方法監控、分析和改進製程的技術。其核心目標是區分過程中固有的、隨機的變異(共同原因變異)和由特定原因引起的、異常的變異(特殊原因變異)。通過識別並消除特殊原因,我們可以使製程達到穩定、可預測的狀態(即〝管制狀態〞),然後再致力於減少共同原因變異,從而實現品質的持續提升。要理解 SPC 如何做到這一點,我們必須首先掌握幾個關鍵的統計學概念。
衡量數據的中心:均值(Mean)
在日常生活中,我們經常使用〝平均〞這個詞。統計學中的均值(Mean),通常指算術平均值(arithmetic mean),是描述一組數據資料的中心位置或中央趨勢最常用的指標。它代表了數據的重心所在。
 圖一、母體及樣本平均值公式
圖一、母體及樣本平均值公式衡量數據的離散程度:標準差(Standard Deviation)
僅僅知道數據的中心位置是不夠的,我們還需要了解數據的分散程度。 標準差(Standard Deviation)就是衡量數據點相對於均值的平均偏離程度的指標。標準差越小,表示數據點越集中在均值附近,製程越穩定;標準差越大,表示數據點越分散,製程波動越大。
 圖二、母體及樣本標準差公式
圖二、母體及樣本標準差公式自然界常見的模式:常態分佈(Normal Distribution)
常態分佈是統計學中的一個基本概念,並且在 SPC 的理論和應用中扮演著特別重要的角色。許多自然現象以及眾多工業和服務製程的輸出,大多遵循常態分佈,尤其是尺寸特性的產品。廣泛使用的休哈特管制圖的管制界限通常是基於製程數據(更具體地說,是樣本平均值)近似常態分佈的假設而建立的。
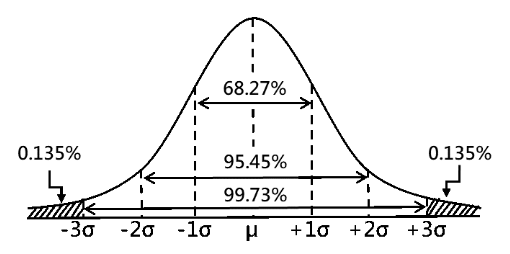 圖三、常態分布
圖三、常態分布
μ:母體之平均值;σ:母體之標準差,常態分佈於μ±σ之間的機率P(Probability)為:
- P(μ-1σ<X<μ+1σ)=0.6827=68.27%
- P(μ-2σ<X<μ+2σ)=0.9545=95.45%
- P(μ-3σ<X<μ+3σ)=0.9973=99.73%
許多 SPC 工具,特別是管制圖的管制界限(通常設置在均值 ±3 個標準差位置,如圖四),其理論依據來自於常態分佈的特性。±3σ(99.73%)範圍幾乎涵蓋了所有由共同原因(Common Cause)引起的隨機變異,因此超出這個範圍點很可能意味著特殊原因(Special Cause)的出現。
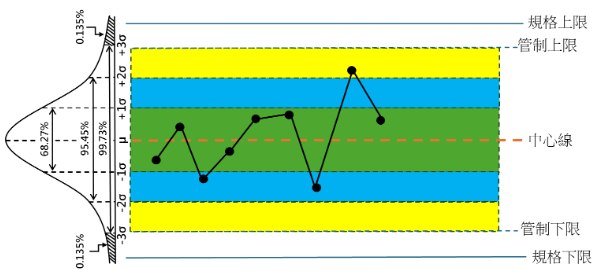 圖四、管制圖與常態分佈對應圖
圖四、管制圖與常態分佈對應圖休哈特博士(Dr. Shewhart)宣稱 變異 存在於製程系統過程中的每個地方,但是可以通過使用簡單的統計工具來瞭解變異,並監控製程的穩定性。大部分工業產品的品質特性數據分配大都符合常態分佈的定律,如能對常態分佈作一個瞭解,在以後應用到統計製程管制(SPC)的一些統計工具時,會更加熟練且有助於提升在 SPC 應用上的敏銳度。